Contenidos (ORD15ENE2021-ESO)
- Geometría del plano.
- Lugar geométrico.
- Cónicas.(no viene en RD)
Criterios de Evaluación (ORD15ENE2021-ESO)
-
3.1. (Peso del criterio 1 punto) Reconocer y describir los elementos y propiedades características de las figuras planas, los cuerpos geométricos elementales y sus configuraciones geométricas.
-
3.2. (Peso del criterio 1/3 punto, porque sólo vemos un estándar de tres en este tema) Utilizar el teorema de Tales y las fórmulas usuales para realizar medidas indirectas de elementos inaccesibles y para obtener las medidas de longitudes, áreas y volúmenes de los cuerpos elementales, de ejemplos tomados de la vida real, representaciones artísticas como pintura o arquitectura, o de la resolución de problemas geométricos. CMCT, CAA, CSC, CEC.
Estándares (ORD15ENE2021-ESO)
-
3.1.1. Conoce las propiedades de los puntos de la mediatriz de un segmento y de la bisectriz de un ángulo, utilizándolas para resolver problemas geométricos sencillos.
-
3.1.2. Maneja las relaciones entre ángulos definidos por rectas que se cortan o por paralelas cortadas por una secante y resuelve problemas geométricos sencillos.
-
3.2.1. Calcula el perímetro y el área de polígonos y de figuras circulares en problemas contextualizados aplicando fórmulas y técnicas adecuadas.
Índice
- Ángulos
- Lugares Geométricos
- Cónicas
- Áreas
Sesiones
Sesión 1 - Lunes 21/02/2022
Introduccción al tema, consulto ideas previas. ¿Qué es un ángulo? ¿Cuánto suman los ángulos de un triángulo?
Hacemos una actividad que consiste en dibujar un triángulo y colorear de diferente color sus ángulos. Después cortamos el triángulo en tres partes, con un ángulo en cada una de estas partes. Ponemos los tres ángulos juntos y comprobamos que forman un ángulo de \( 180^o \) .

Sesión 2 - Martes 22/02/2022
- Pregunto ideas previas sobre el concepto de polígono.
- Definimos linea poligonal y a partir de ahí definimos qué es un polígono.
- Explico la fórmula de la Suma de ángulos interiores de un polígono = 180*(n-2). Pongo ejemplo del triángulo que vimos ayer para que comprueben que funciona. Después vamos a los cuadriláteros y vemos que tiene que ser \( 360^o \). Hacemos la siguiente actividad práctica para comprobarlo.
- Dibujamos dos cuadrilateros iguales, coloreando sus cuatro ángulos de diferente color. Uno lo pegamos directamente en la hoja del cuaderno y otro lo cortamos con las tijeras separando sus cuatro ángulos. Después unimos esos ángulos y se observa que forman un ángulo de \( 360^o \) circunferencia completa.
Sesión 3 - Miércoles 23/02/2022
- Recordamos la fórmula de la suma de los ángulos interiores vista ayer. Pongo ejemplo con pentágono, hexágono, etc.
- Explico los ángulos centrales e inscritos en una circunferencia y la relación que existe entre ambos si comparte el mismo arco. *(ángulo central = 2 inscrito) **.
- Todos los ángulos inscritos que abarcan el mismo arco.
- Act 1: ¿Cuál es la medida angular de cada uno de los ocho arcos iguales en que se ha dividido la circunferencia siguiente? Indica razonadamente cuánto miden los ángulos señalados.
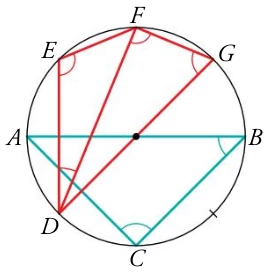
Sesión 4 - Jueves 24/02/2022
Repasamos la actividad 1 de ayer. Con esta actividad aclarada hacemos la siguiente:
- Act 2: ¿Cuál es la medida angular de cada uno de los diez arcos iguales en que se ha dividido la circunferencia siguiente? Indica razonadamente cuánto miden los ángulos señalados.
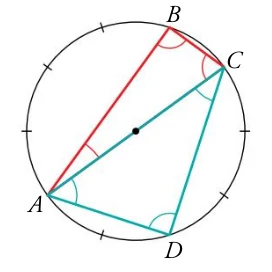
Sesión 5 - Miércoles 2/03/2022
En las actividades 3, 4 y 5 indica razonadamente cuánto miden los ángulos señalados:
| Act 3: | Act 4: |
|---|---|
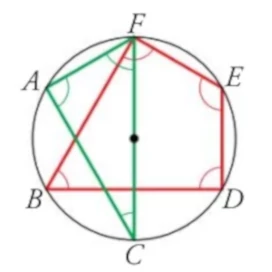 |
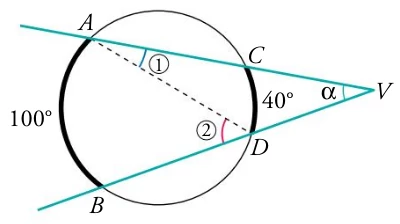 |
| Act 5: |
|---|
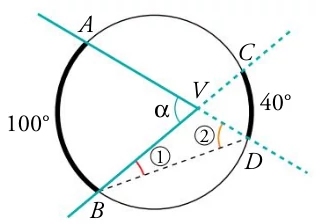 |
Lugares geométricos y ejemplos:
- Un lugar geométrico es el conjunto de puntos del plano que verifica cierta propiedad. A continuación vemos tres ejemplos:
| Mediatriz de un segmento | Bisectriz de un ángulo |
|---|---|
| Es el lugar geométrico de los puntos del plano cuya distancia a los extremos del segmento es la misma. | Es el lugar geométrico de los puntos del plano cuya distancia a los lados del ángulo es la misma. |
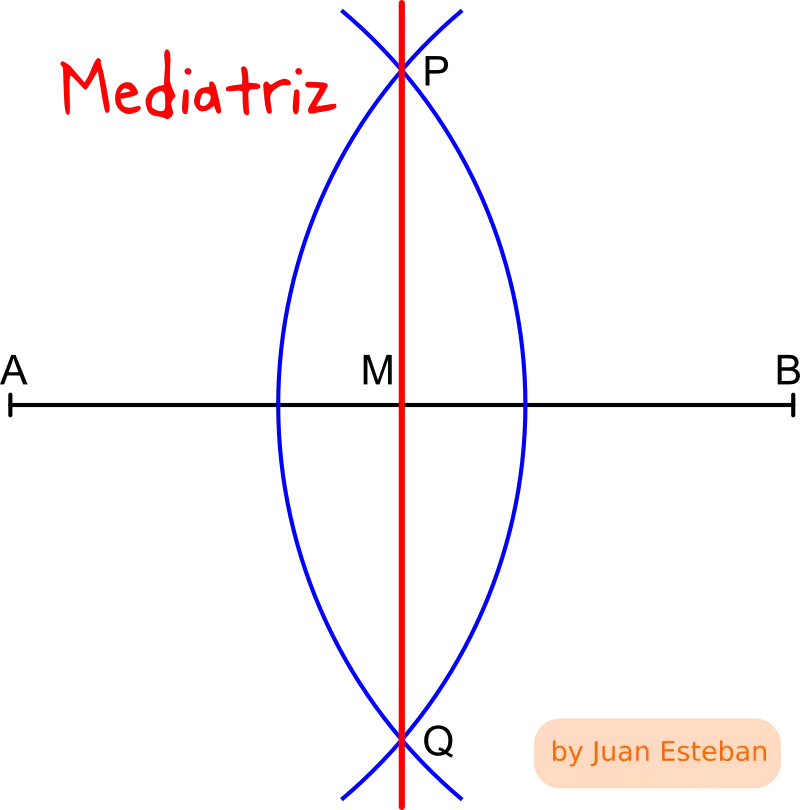 |
 |
- La circunferencia es el lugar geométrico de los puntos del plano cuya distancia a un punto fijo llamado centro es constante.
Sesión 6 - Jueves 3/03/2022
Repasamos al inicio la sesión anterior.
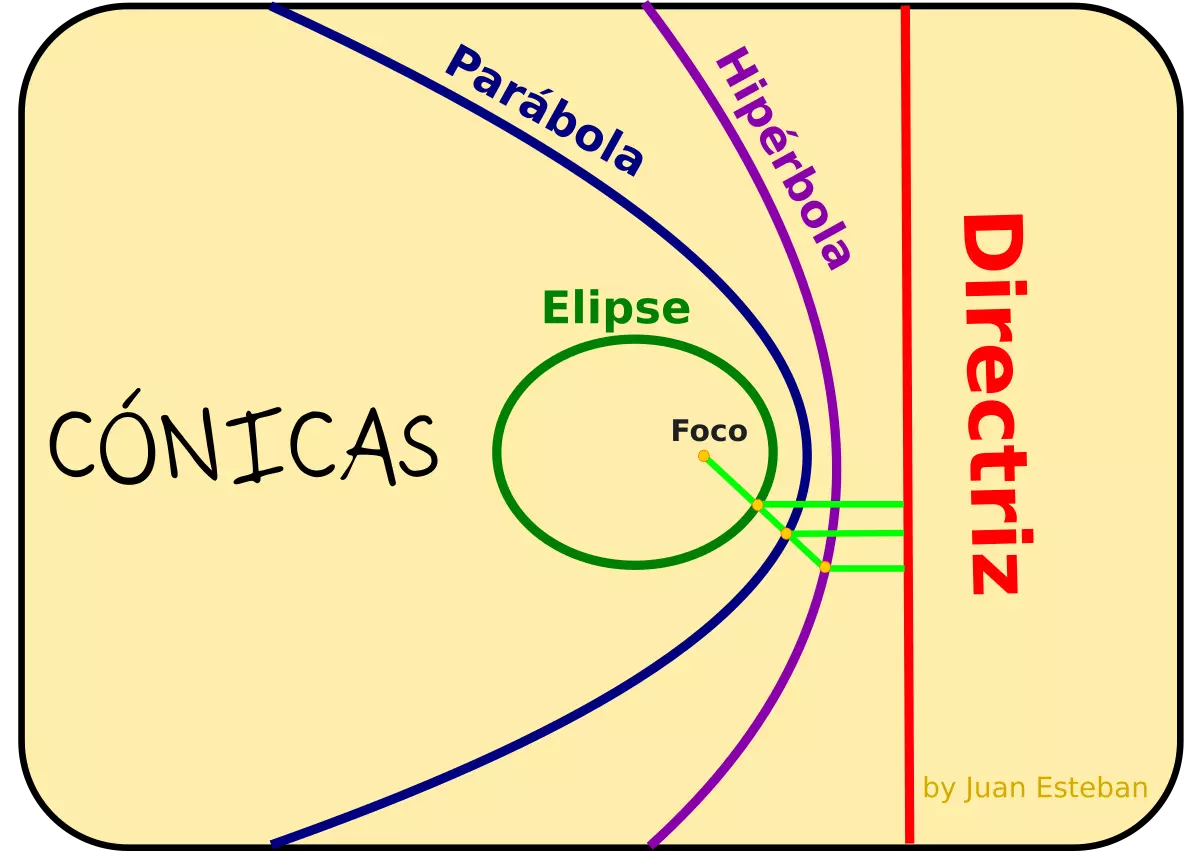
Cónicas.
Una cónica es el lugar geométrico de los puntos del plano cuyo cociente de distancias a un punto fijo llamado foco y a una recta llamada directriz es constante. A esta constante se le llama excentricidad e de la cónica.
- Si e<1 se llama elipse.
- Si e=1 la cónica se llama parábola.
- Si e>1 se llama hipérbola.
Sesión 7 - Lunes 7/03/2022
Definiciones habituales de cónicas en el plano:
- Elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.
- Hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias, en valor absoluto, a dos puntos fijos llamados focos es constante.
- Parábola es el lugar geométrico de los puntos del plano cuya distancia a un punto fijo llamado foco coincide con la distancia a una recta llamada directriz.
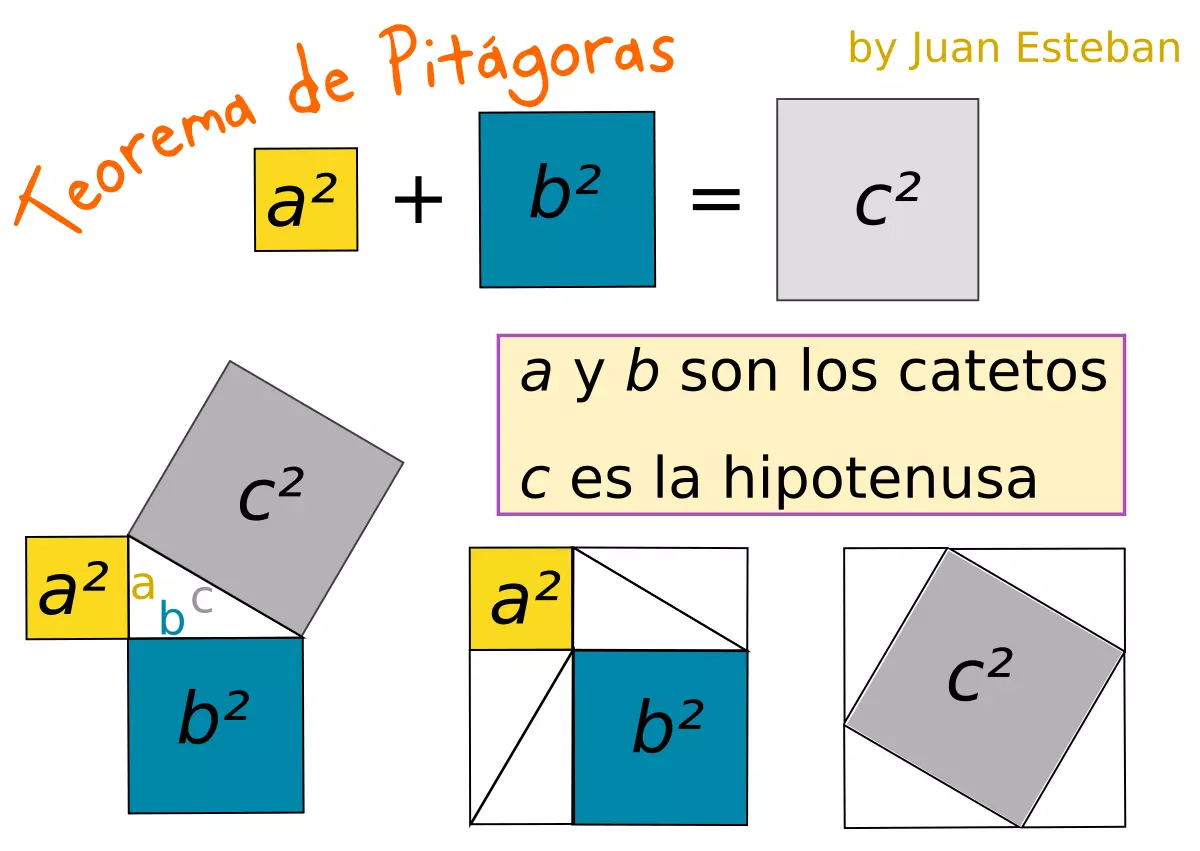
Repaso Teorema de Pitágoras
Introducimos la fórmula del teorema de Pitágoras que trataremos en la siguiente sesión.
Martes 8/03/2022
Día internacional de la mujer.
Sesión 8 - Miércoles 9/03/2022
El teorema de Pitágoras es una herramienta magnífica que usamos para resolver muchos problemas de distancias.
- Act 9: Calcula el valor de x en cada caso:
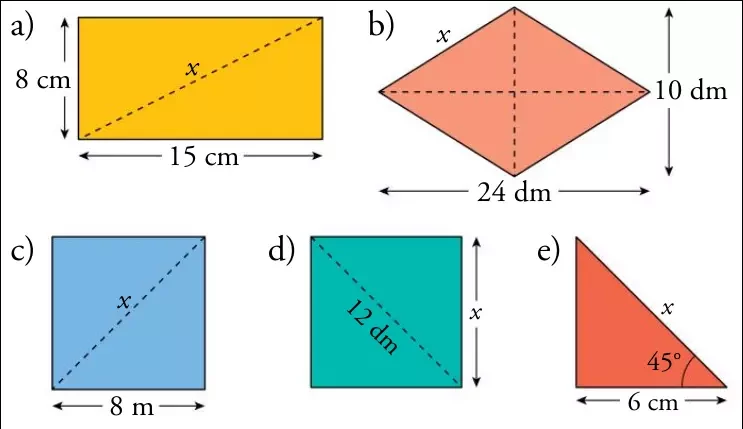
Sesión 10 - Jueves 10/03/2022
Trabajamos los primeros apartados de la actividad 10.
- Act 10: Calcula el valor de x en cada caso:
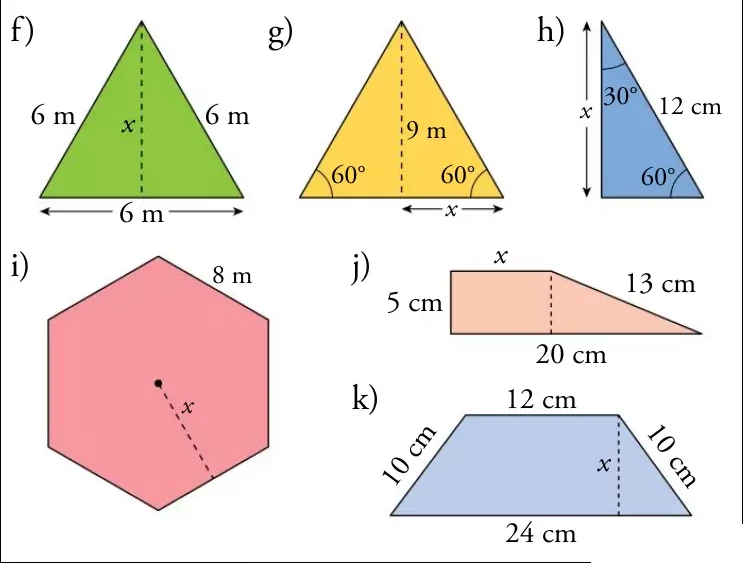
Áreas de polígonos:
Explico las áreas de las siguientes figuras:
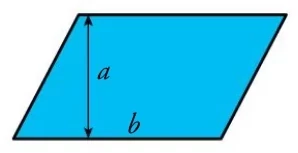
| Rectángulo | Romboide | Rombo |
|---|---|---|
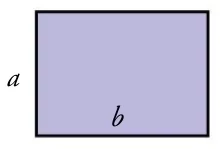 \[ \large A= base \cdot altura \] \[ \large A= base \cdot altura \] |
 \[ \large A= base \cdot altura \] \[ \large A= base \cdot altura \] |
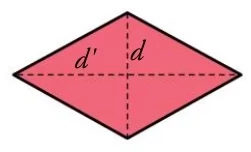 \[ \large A= \frac{d \cdot d^\prime}{2} \] \[ \large A= \frac{d \cdot d^\prime}{2} \] |
| Triángulos | Trapecio | Polígono Regular |
|---|---|---|
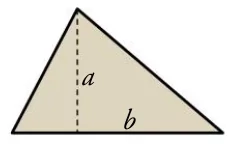 \[ \large A= \frac{base \cdot altura}{2} \] \[ \large A= \frac{base \cdot altura}{2} \] |
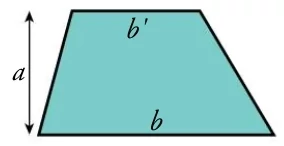 \[ \large A= \frac{b + b^\prime}{2} \cdot altura\] \[ \large A= \frac{b + b^\prime}{2} \cdot altura\] |
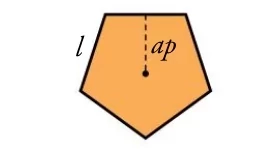 \[ \large A= \frac{\textit{perímetro} \cdot apotema}{2} \] \[ \large A= \frac{\textit{perímetro} \cdot apotema}{2} \] |
Sesión 11 - Lunes 14/03/2022
Terminamos las actividades del teorema de Pitágoras de la actividad 10.
- Act 10: Calcula el valor de x en cada caso:

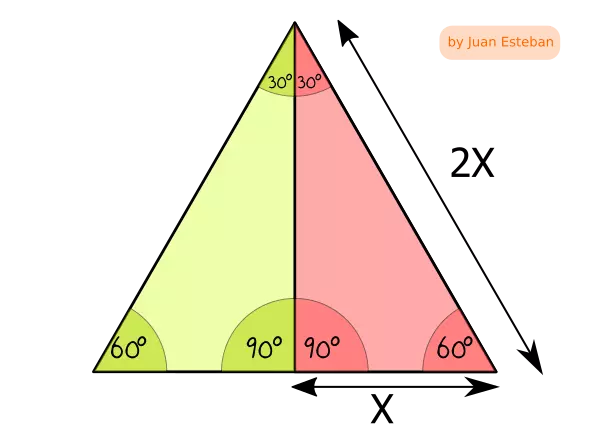
Hago hincapié en que un cartabón es un triángulo rectángulo cuyos ángulos son 90, 60 y 30 grados. También les muestro que con dos cartabones juntos se puede formar un triángulo equilátero. En la resolución de los ejercicios hacemos uso de que la hipotenusa del cartabón es el doble del cateto menor. En la figura de abajo el cateto menor mide x, y la hipotenusa mide 2x
Sesión 12 - Martes 15/03/2022
Áreas de figuras curvas:
| Círculo | Sector Circular | Corona Circular |
|---|---|---|
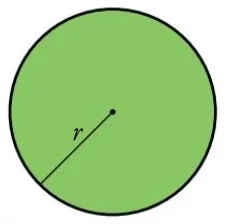 \[ \large A= \pi \cdot r^2 \] \[ \large A= \pi \cdot r^2 \] |
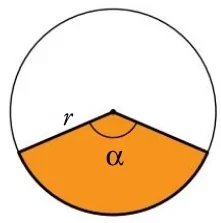 Es la fracción \(\alpha\)/360o del área del círculo completo.\[ \large A= \frac{\alpha}{360} \cdot \pi \cdot r^2 \] Es la fracción \(\alpha\)/360o del área del círculo completo.\[ \large A= \frac{\alpha}{360} \cdot \pi \cdot r^2 \] |
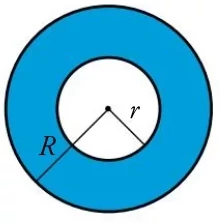 Es el área del círculo grande menos el área del círculo chico.\[ \large A= \pi \cdot (R^2-r^2) \] Es el área del círculo grande menos el área del círculo chico.\[ \large A= \pi \cdot (R^2-r^2) \] |
| Elipse | Segmento de parábola |
|---|---|
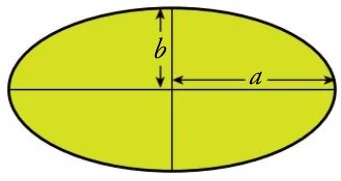 \[ \large A= \pi \cdot a \cdot b \] Observa que si \(a=b\) entonces obtenemos el área de un círculo. \[ \large A= \pi \cdot a \cdot b \] Observa que si \(a=b\) entonces obtenemos el área de un círculo. |
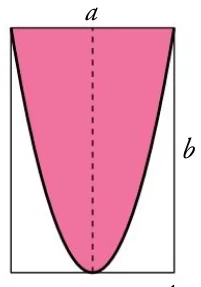 Es 2/3 del área del rectángulo. \[\large A = \frac{2}{3} \cdot a \cdot b\] Es 2/3 del área del rectángulo. \[\large A = \frac{2}{3} \cdot a \cdot b\] |
Sesión 13 - Miércoles 16/03/2022
Trabajamos la actividad 12, con algo de dificultad porque se nos fue incluso la luz.
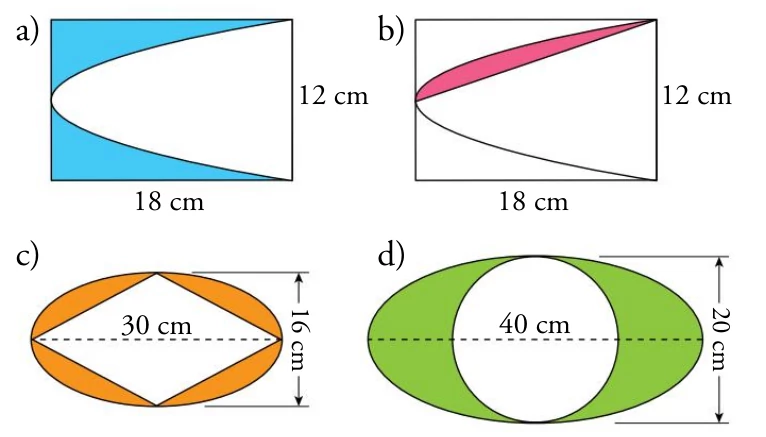
- Act 12: Calcula el área coloreada de las siguientes figuras curvas:
Sesión 14 - Jueves 17/03/2022
-
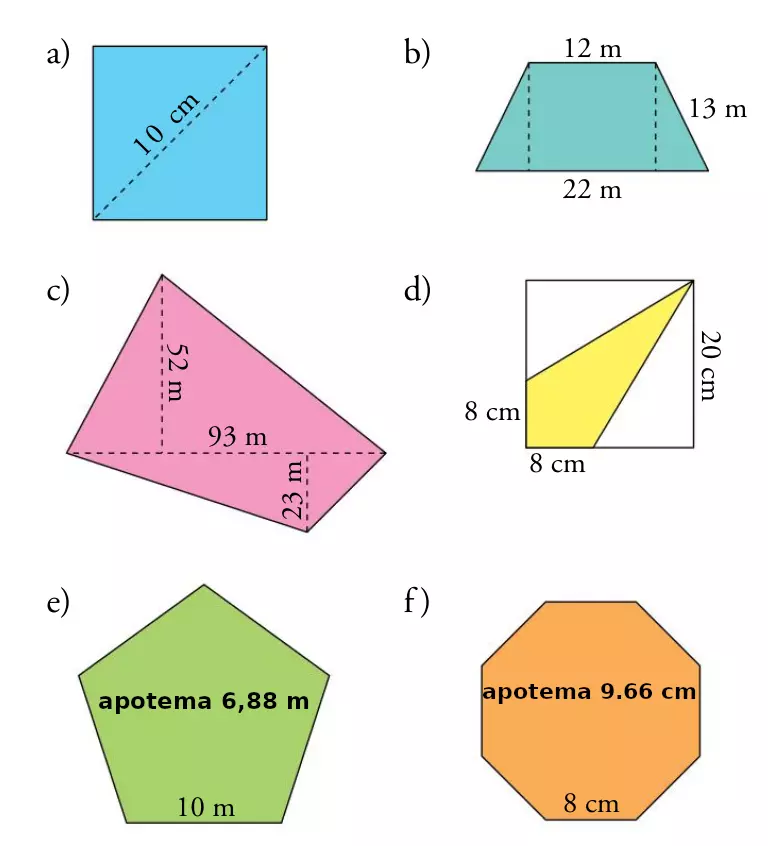
Act 11: Calcula el área de los siguientes polígonos:
-
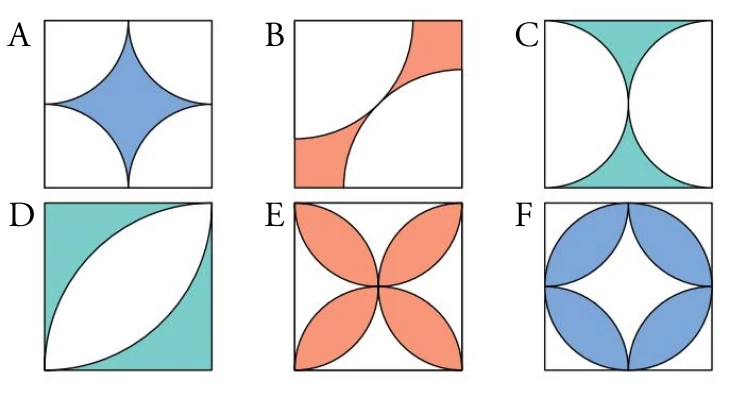
Act 13: Estos cuadrados tienen 1 metro de lado. Calcula en cm2 el área coloreada:
Sesión 15 - Lunes 21/03/2022
Repaso del tema y resolución de dudas.
No hay clase porque hay un taller de periodismo.
Sesión 16 - Martes 22/03/2022
Prueba escrita.