Contenidos (ORD15ENE2021-ESO)
- Teorema de Tales. División de un segmento en partes proporcionales. Aplicación a la resolución de problemas.
Criterios de Evaluación (ORD15ENE2021-ESO)
-
3.2. (Peso del criterio 2/3 punto, porque sólo vemos un estándar de tres en este tema) Utilizar el teorema de Tales y las fórmulas usuales para realizar medidas indirectas de elementos inaccesibles y para obtener las medidas de longitudes, áreas y volúmenes de los cuerpos elementales, de ejemplos tomados de la vida real, representaciones artísticas como pintura o arquitectura, o de la resolución de problemas geométricos. CMCT, CAA, CSC, CEC.
-
3.3.(1 punto) Calcular (ampliación o reducción) las dimensiones reales de figuras dadas en mapas o planos, conociendo la escala. CMCT, CAA.
Estándares (ORD15ENE2021-ESO)
-
3.2.2. Divide un segmento en partes proporcionales a otros dados y establece relaciones de proporcionalidad entre los elementos homólogos de dos polígonos semejantes.
-
3.2.3. Reconoce triángulos semejantes y, en situaciones de semejanza, utiliza el teorema de Tales para el cálculo indirecto de longitudes en contextos diversos.
-
3.3.1. Calcula dimensiones reales de medidas de longitudes y de superficies en situaciones de semejanza: planos, mapas, fotos aéreas, etc.
Índice
- Semejanza
- Definición.
- Aplicación a áreas.
- Aplicación a volúmenes.
- Teorema de Thales
- Enunciado del teorema.
- Triángulos en posición de Thales.
- División de un segmento en partes iguales.
- Escala, planos y mapas
Sesiones
Sesión 1 - Lunes 20/03/2022
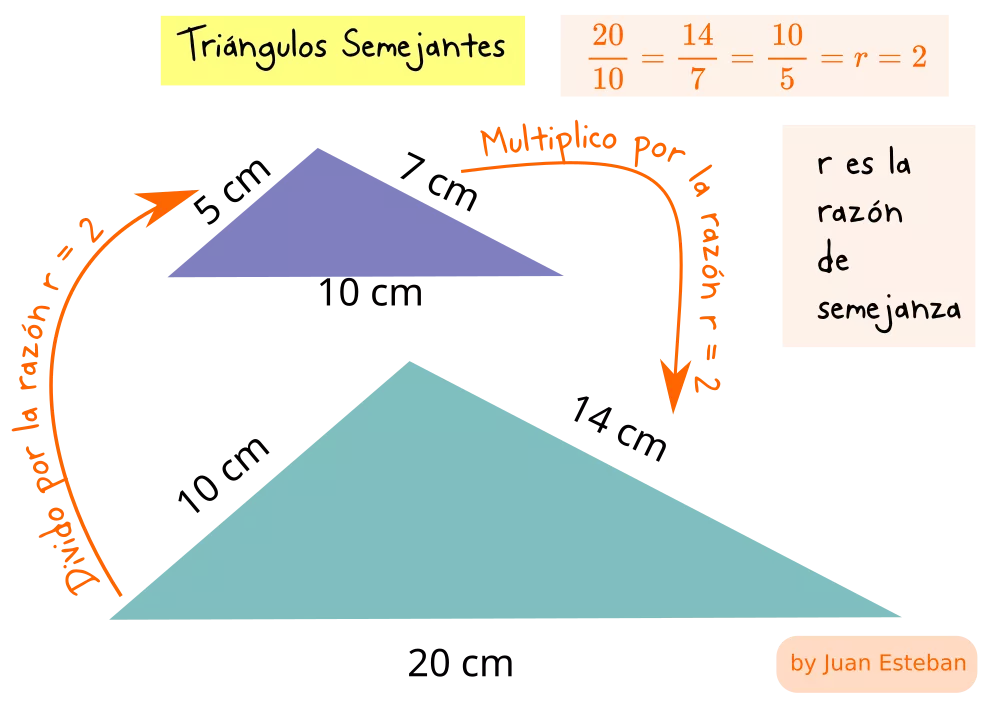
Semejanza: Dos figuras son semejantes, si tienen la misma forma. Si aplicamos esta idea a los polígonos , diremos que dos polígonos son semejantes si tienen lados proporcionales y ángulos iguales.
La razón de semejanza entre dos figuras, es el número por el que multiplico las medidas de una figura 1, para transformarla en la figura 2. Suele denotarse por la letra r.
-
Si r>1 estamos ampliando la figura.
-
Si r<1 estamos reduciendo la figura.
-
La razón entre áreas de figuras semejantes es r2.
-
La razón entre volúmenes de figuras semejantes es r3
Regla mnemotécnica, la razón será siempre rnº de dimensiones. Si son tres dimensiones (volumen) r3, si son dos dimensiones r2 y si es una dimensión r.
Act-1: Considera el rectángulo 2x6 cm y amplíalo con razón de semejanza r=3. Calcula las áreas de dichos rectángulos y responde a la pregunta ¿cuál es la razón entre ambas?
Miércoles 23/03/2022
- Taller de periodismo.
Jueves 24/03/2022
- Huelga estudiantes.
Sesión 2 - Lunes 28/03/2022
- Recordamos la clase del lunes pasado.
- Vemos el enunciado del teorema de Thales y hacen actividad para comprobar las medidas con regla y cartabón.
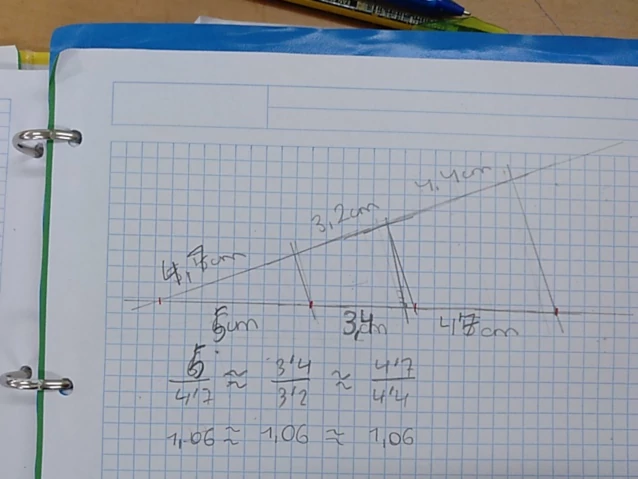
Sesión 3 - Martes 29/03/2022
Hoy practicaremos la razón de semejanza con estas actividades.
Practica con las siguientes actividades de Thales:
1. 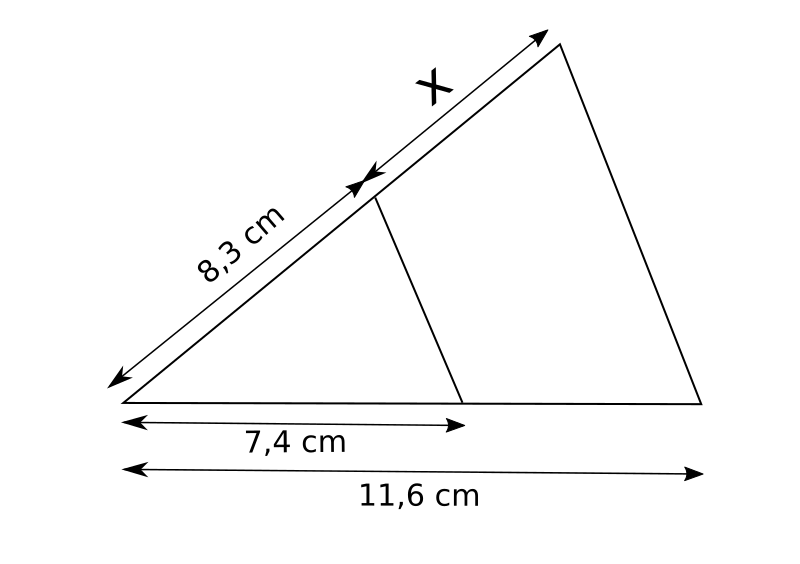 2.
2. 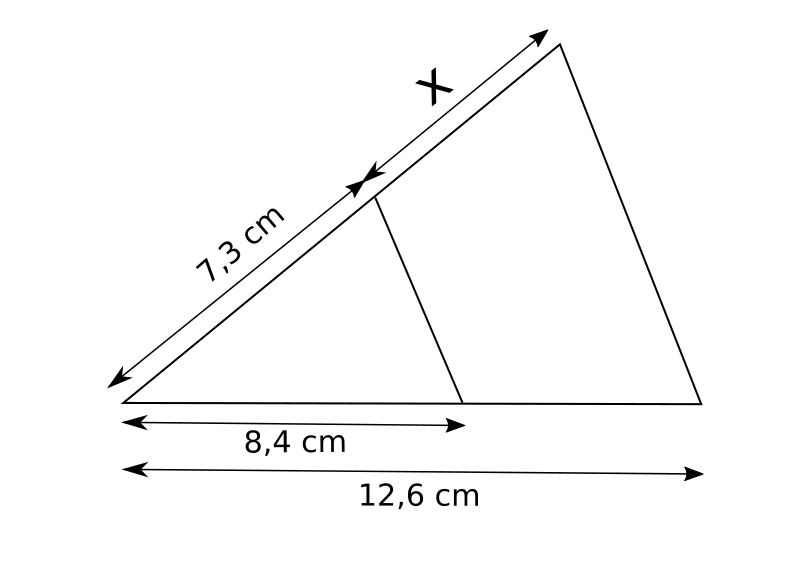 3.
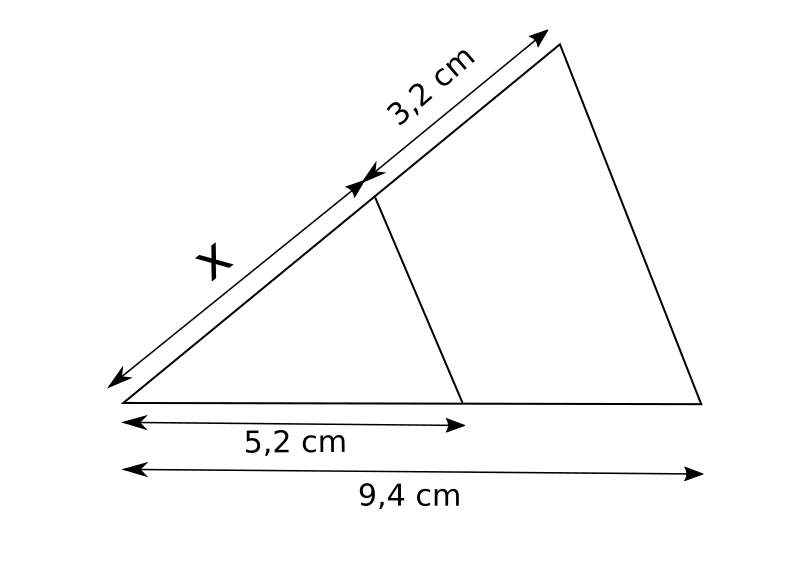
3. 
Sesión 4 - Miércoles 30/03/2022
4. 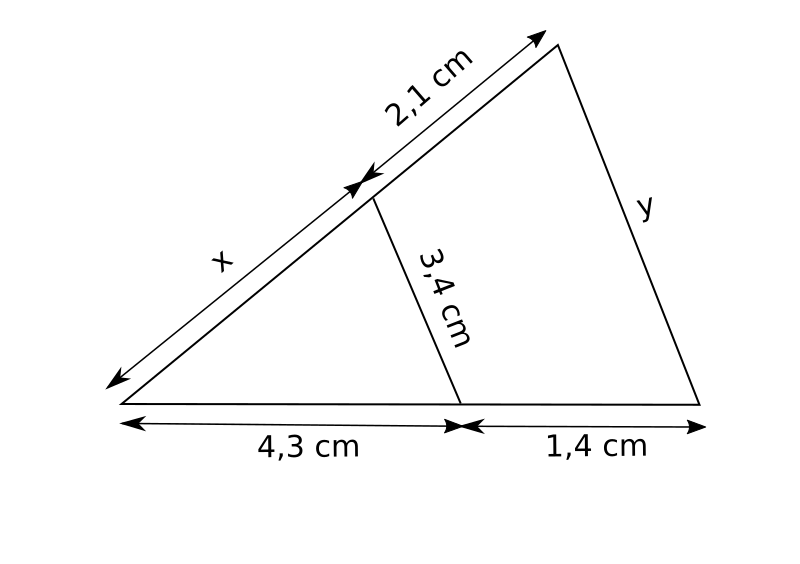 5.
5. 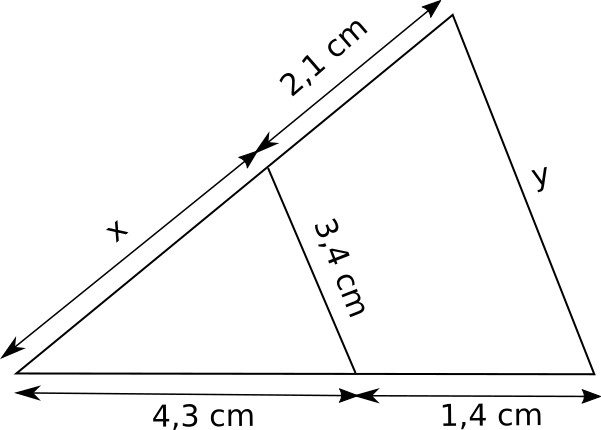 6.
6. 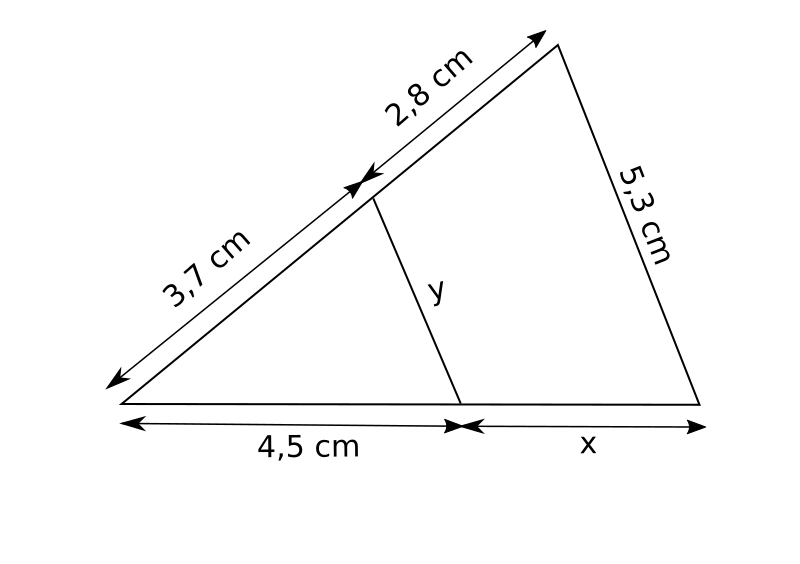 7.
7. 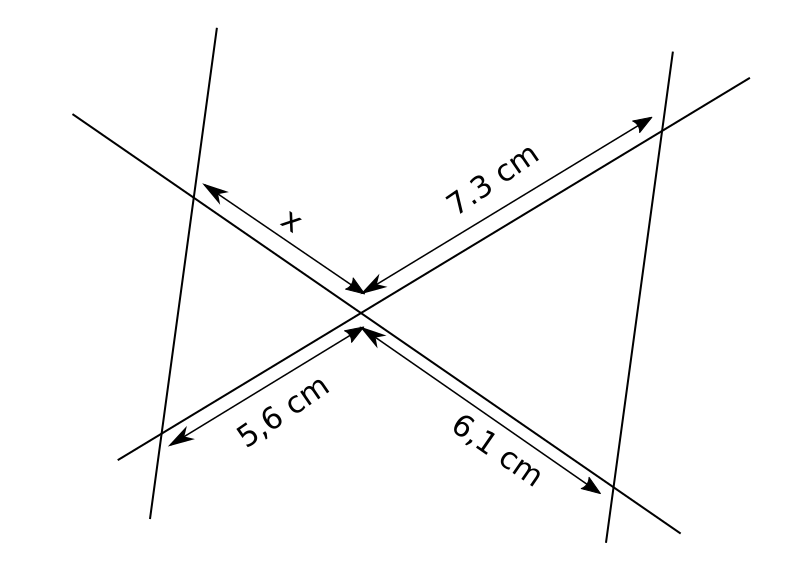 8.
8. 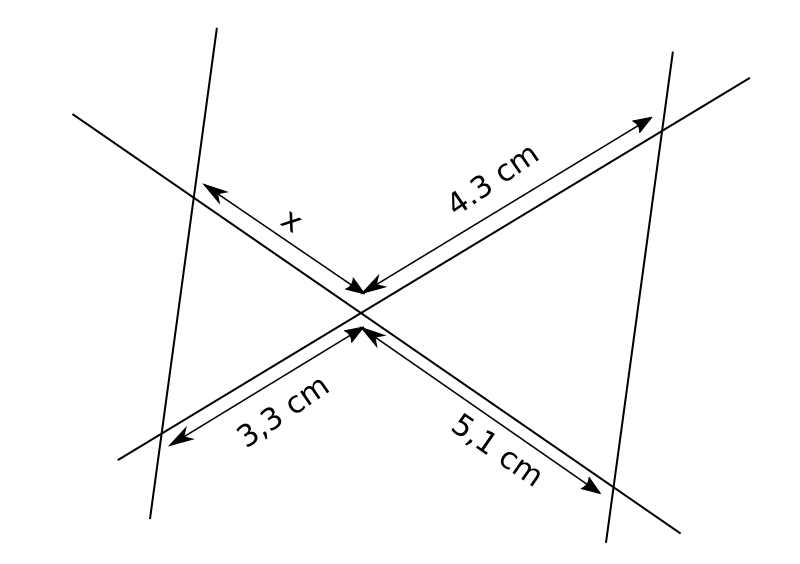 9.
9. 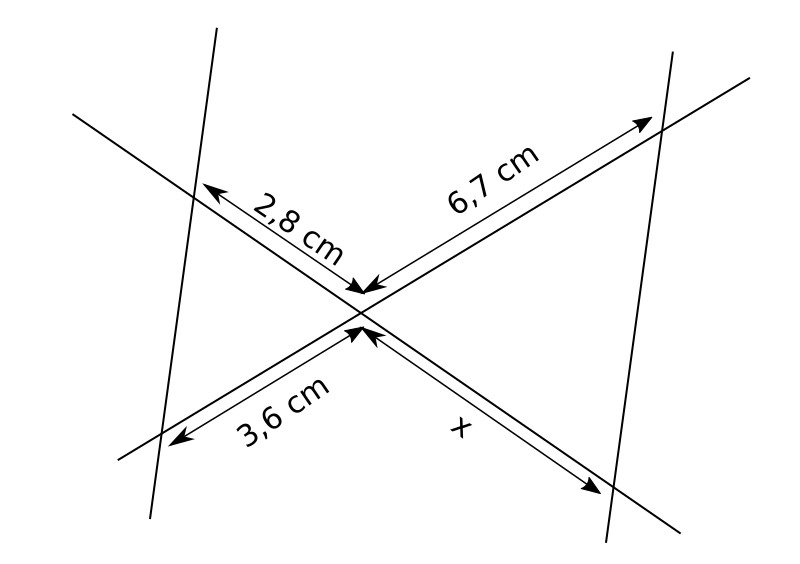 10.
10. 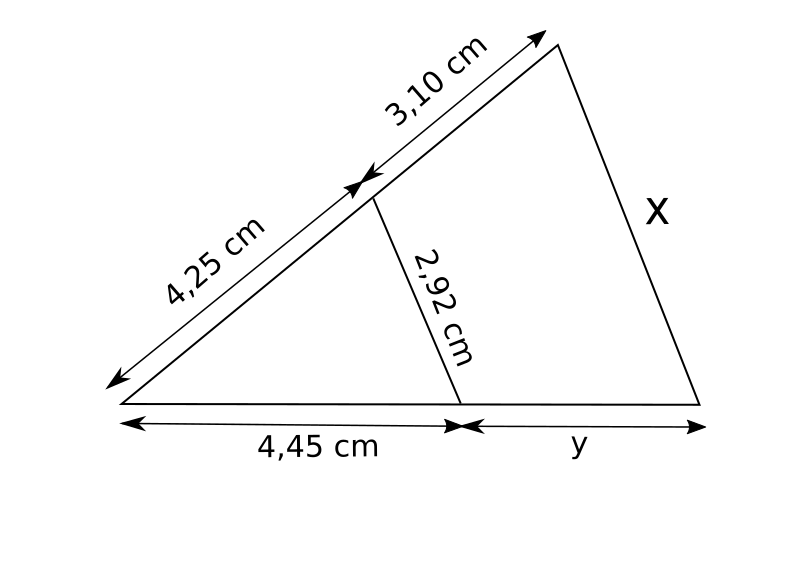 11.
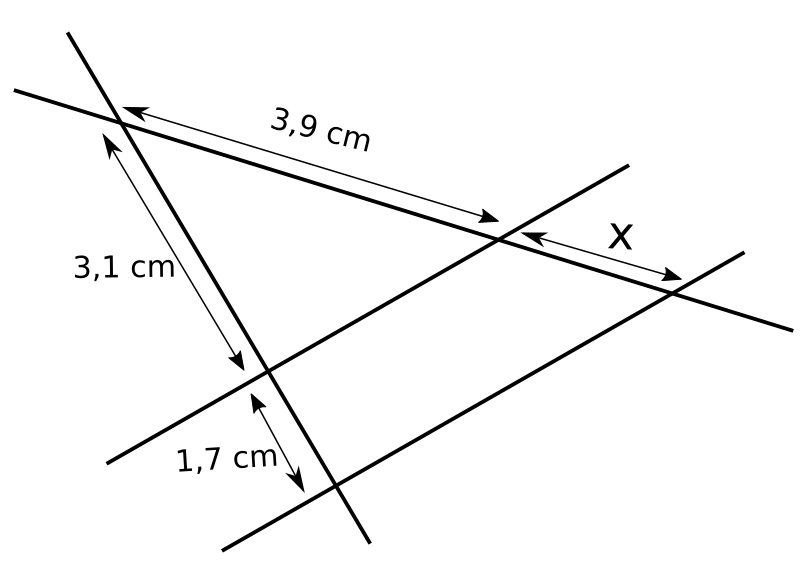
11. 
Semana Santa
Sesión 5 - Lunes 18/04/2022
12. Para calcular la altura de un árbol, Eduardo ve la copa reflejada en un charco y toma las medidas que indica el dibujo. ¿Cual es la altura del árbol?
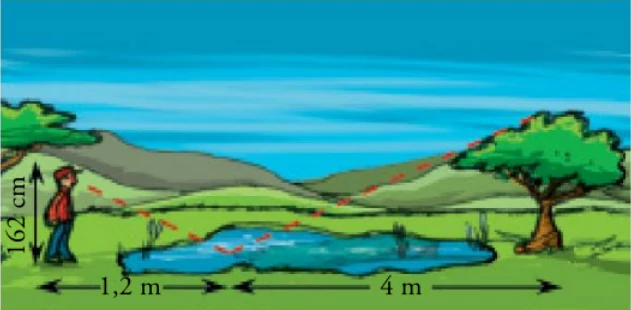
13. ¿Cual es la profundidad de un pozo, si su anchura es 1,5 m y alejándote 0,5 m del borde, desde una altura de 1,7 m, observas que la visual une el borde del pozo con la línea del fondo?

Sesión 11 - Lunes 19/04/2022
14. Calcula la altura del edificio:
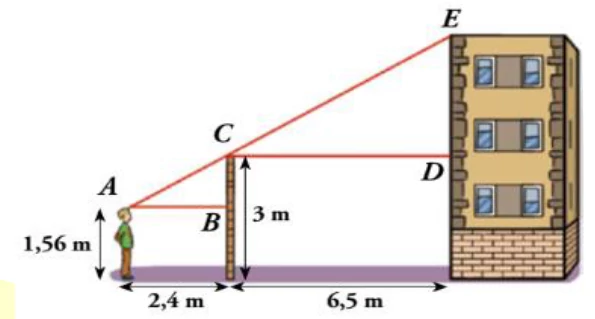
15. Calcula la altura de un molino eólico, sabiendo que su sombra mide 25 m y ue en ese mismo instante un objeto de 1,5 m proyecta una sombra de 1,2 m.

16. Calcula la altura de las torres de Hércules en Los Barrios (Cádiz), sabiendo que su sombra mide 42 m y que en ese mismo instante una persona de 1,74 m proyecta una sombra de 58 cm.

17. Calcula la altura de la torre Eiffel de París sabiendo que cuando su sombra es de 233,58 m, la sombra de una persona de 1,75 m es 1,25 m. Redondea el resultado a metros.

18. Observa la valla del dibujo. Si en el lado inclinado la medida correspondiente a 20 cm es 25 cm, calcula las
medidas de las distancias de los restantes barrotes.
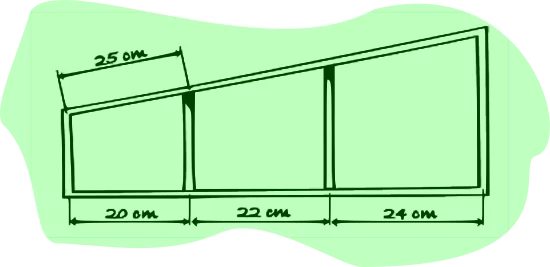
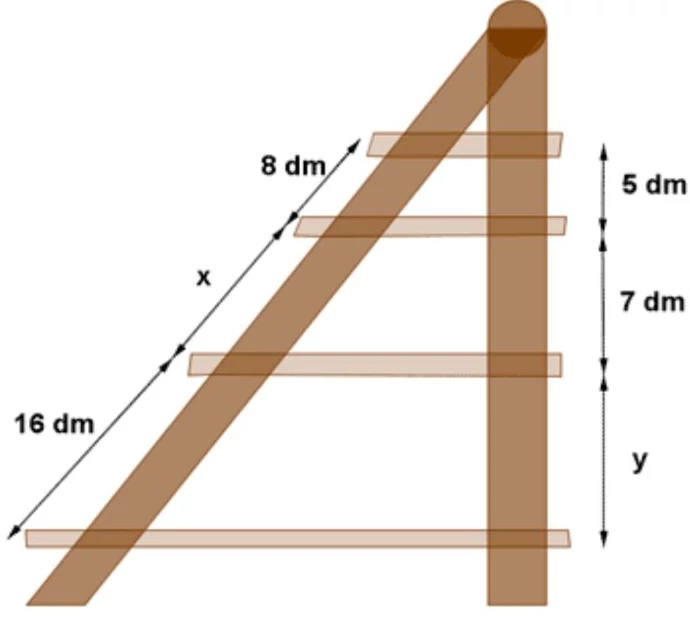
19. Las baldas de una repisa representada en la figura son paralelas. Calcula las longitudes de la repisa representadas como x e y.
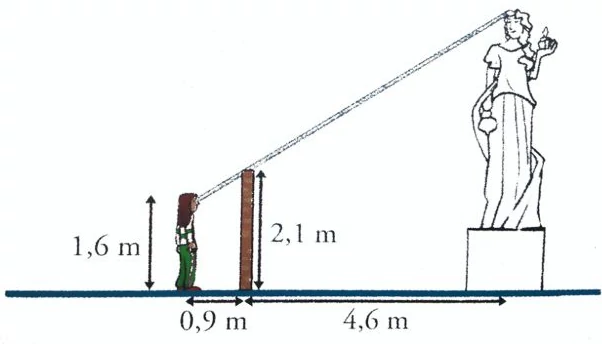
20. A qué altura se encuentra el extremo superior de la escultura, sabiendo que Paula la ve alineada con el borde de la valla.
Sesión 12 - Martes 20/04/2022
Prueba escrita.